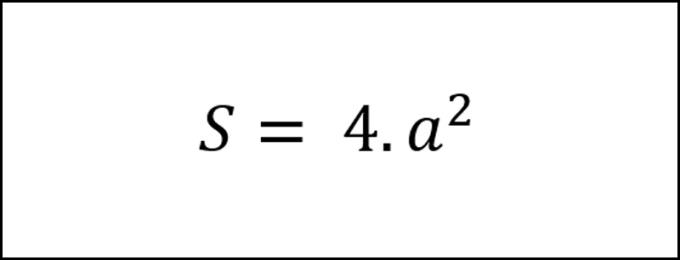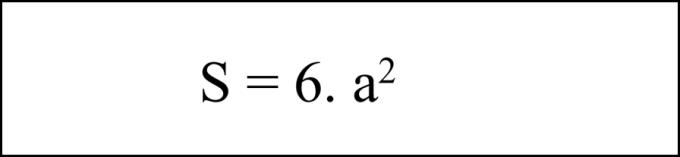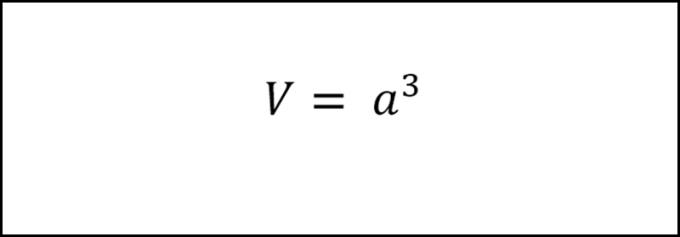क्यूब 3 डी ज्यामितीयों में से एक है जो रोजमर्रा की जिंदगी में अक्सर दिखाई देता है। क्यूब के क्षेत्र के लिए अवधारणाएं, गुण, सूत्र हैं, साथ ही साथ इसकी मात्रा भी। इसके अलावा, गणना करते समय यह अत्यंत उपयोगी गणना भी लाता है।
1. अवधारणाओं और गुण क्यूब्स
- अवधारणा
एक घन एक पहेली है जिसमें 6 चेहरे, 8 कोने, 12 किनारे हैं, सभी चेहरे समान वर्ग, समान पक्ष हैं। एक घन को बराबर चौड़ाई, लंबाई और ऊंचाई वाले घन के रूप में समझा जा सकता है।
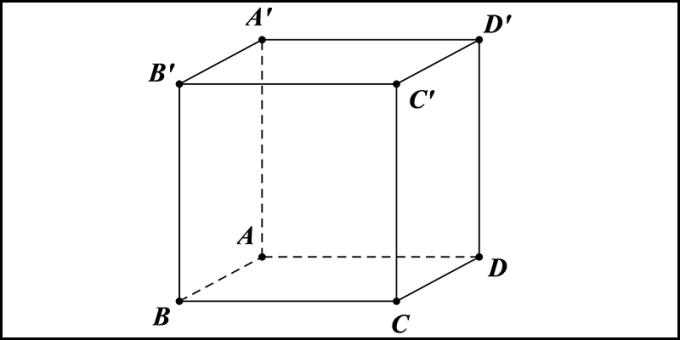
- घन के गुण
+ 6 सममित और समान विमान हैं।
+ 12 बराबर किनारे हैं।
+ पक्षों का विकर्ण बराबर है।
+ विकर्ण क्यूब्स बराबर हैं।
2. एक घन के क्षेत्र की गणना करने के लिए सूत्र
- क्यूब के आसपास के क्षेत्र की गणना करने के लिए सूत्र
क्यूब के आसपास का क्षेत्र एक तरफ की लंबाई के वर्ग के बराबर है जिसे चार से गुणा किया जाता है।
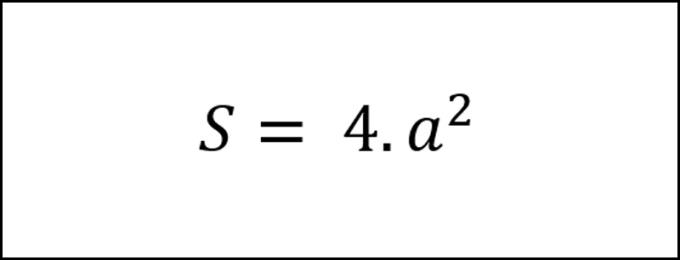
जिसमें :
+ a: एक पक्ष की लंबाई है।
+ एस: आसपास का क्षेत्र है।
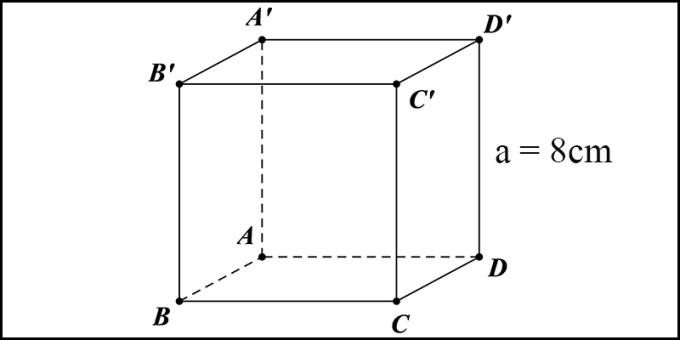
यहाँ, WebTech360 आपको सूत्र को लागू करने के लिए आसान बनाने के लिए आपको एक उदाहरण देगा। बता दें कि A'B'C'D'.ABCD के घन की लंबाई 8 सेमी है। इसके आसपास के क्षेत्र की गणना करें।
सूत्र लागू करना। हमारे पास: S = 4 xaxa = 4 x 8 x 8 = 256 (cm2)।
- क्यूब के कुल क्षेत्रफल की गणना के लिए सूत्र
क्यूब का कुल क्षेत्रफल एक तरफ की लंबाई के वर्ग के बराबर है जिसे छह से गुणा किया जाता है।
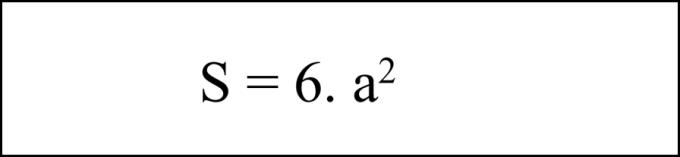
जिसमें :
+ a: एक पक्ष की लंबाई है।
+ एस: कुल क्षेत्र है।

उदाहरण: एक नीले घन को देखते हुए जो एक तरफ 10 सेमी है। ऊपर की छवि के कुल क्षेत्र की गणना करें।
उपरोक्त सूत्र को लागू करने के लिए हमारे पास S = 6 x 10 x 10 = 600 (cm2) है।
3. एक घन की मात्रा की गणना के लिए सूत्र
घन का आयतन एक भुजा की लंबाई के घन के बराबर होता है।
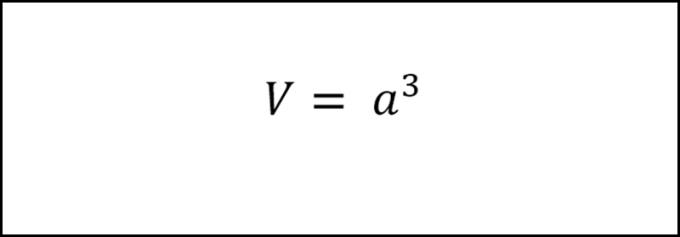
जिसमें :
+ a: एक पक्ष की लंबाई है।
+ V: वॉल्यूम है।
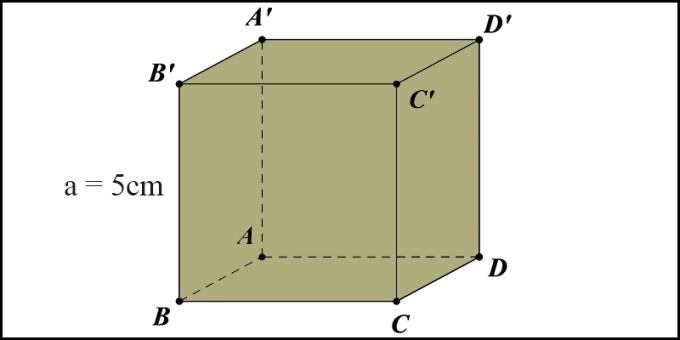
वॉल्यूम गणना के लिए संदर्भ उदाहरण। चलो A'B'C'D'.ABCD लंबाई BB '= 5 सेमी। घन की मात्रा की गणना करें।
हमारे पास सूत्र लागू करने के लिए V = axaxa = 5 x 5 x 5 = 125 (cm3) है।
4. क्यूब व्यायाम करते समय ध्यान दें
- ब्लॉक द्वारा गणना की गई मात्रा की इकाइयाँ (उदाहरण घन मीटर (एम 3))।
- माप घातीय 2 (जैसे वर्ग मीटर (एम 2)) की इकाइयों में गणना की गई इकाई क्षेत्र।
उम्मीद है कि लेख उपयोगी ज्ञान लाएगा। सौभाग्य!